커패시터와 커패시턴스

커패시턴스

용량성 소자라고도 불리는 커패시터는

위 그림과 같이 절연 물질인 유전체의 위 아래에 금속판을 붙인 형태의 소자를 지칭합니다. 두 금속판에는 도선이 연결되어 있구요. 금속판 사이는 절연체로 채워져 있습니다.

이러한 커패시터의 두 금속판에 전압을 인가하게 되면 전기적으로 발생하는 인력과 척력에 의해 전하의 이동이 발생하지만, 절연체로 인해 금속판 사이로는 이동할 수 없으므로 두 금속판의 전위차가 점점 커지게 됩니다.

커패시터의 양단에 전압을 인가하는 동안에는 두 금속판이 계속해저 전기적인 극성을 띄게 되겠지만, 인가되었던 전압을 끊어주게 되면 전기적 평형 상태로 돌아가기 위해 모여있던 전하들이 원래 자리로 이동하게 됩니다.

커패시터의 특성을 간략하게 알아보았으니, 물리적인 특성에 대해 본격적으로 파악해 봅시다. 커패시터의 양단에 전압을 인가했을 때 축적되는 전하량은 동일한 물성의 커패시터를 기준으로, 걸리는 전압의 크기에 비례할 것입니다. 즉,

와 같은 식으로 표현할 수 있구요. 이 식에서 사용된 비례 상수 C가 커패시터 소자의 특성에 해당하는 커패시턴스가 됩니다. (단위는 패럿 [F]를 사용합니다.) 커패시터는 실제 생긴 모양을 본따 두 개의 평형 금속판을 가까이 둔 것과 같은 형태로 회로 안에서 표현되구요. 축적되는 전하량에 대한 관계식을

의 전류에 대한 관계식에 대입하면,

의 관계식을 유도할 수 있습니다.

멀티심을 이용해서 지금까지 설명드린 내용을 확인해 보겠습니다.

위 그림과 같은 회로를 구성하구요. 자체적인 스위칭 효과를 주기 위해 크기가 5[V], 주기가 500ms인 펄스 형태의 전압원을 회로에 연결하였습니다. 그리고 커패시터의 양단에 프로브를 연결해서 전압을 측정해 보면,

위와 같은 결과를 얻을 수 있습니다. 여기서 전압원의 한 주기에 대한 시뮬레이션 결과를 해석해 보자면, 5[V]의 전압을 막 공급하였을 때는 정상적으로 전하들이 이동하게 됩니다. 당연히 커패시터의 금속판에도 전하가 조금씩 축적되기 때문에 전위차가 서서히 나타나기 시작하구요. 커패시터에 축적된 전하가 많아질수록 (전위차가 점점 커질수록) 회로에 흐르는 전류의 크기가 서서히 작아지다가, 공급 전압의 크기와 같은 크기의 전위차가 커패시터 양단에 생기게 되면 마치 스위치를 끊어버린 것처럼 회로의 전류가 차단됩니다.

반대로, 회로에 걸리던 전압이 0[V]가 되면, 커패시터에 축적되어 있던 전하들이 전기적 평형 상태를 이루기 위해 원래의 자리로 돌아가게 되면서 반대 방향으로 전류가 흐르게 됩니다. 이 현상은 커패시터에 축적되었던 전하들이 모두 이동할 때까지 계속되구요. 양쪽의 금속판이 전기적으로 중성 상태가 되면, 더 이상의 전하 이동이 생기지 않으므로 회로에 흐르던 전류도 다시 0[A]가 됩니다.

---

합성 커패시턴스

저항과 마찬가지로, 회로 안에서 여러 개의 커피시터를 연결해서 사용할 수 있습니다. 그리고, 여러 개의 커패시터가 사용되었지만, 회로를 해석하는 과정에서 하나의 커패시터가 연결된 회로처럼 등가 변환할 수 있는데요.

2개의 커패시터가 직렬로 연결된 회로에 전압 v(t)를 가해서 i(t)의 전류가 흘렀다고 한다면,

각 커패시터의 전위차에 대해 위 식과 같은 키르히호프 전압 법칙이 적용됩니다. 위에서 설명한 커패시터의 전압, 전류 관계식을

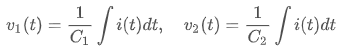
위 식과 같이 전압에 관한 형태로 변환하여 키르히호프 전압 법칙에 적용하면

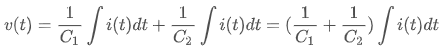
으로 정리할 수 있구요. 크기가 C_eq인 커패시터의 양단에 같은 크기의 전압을 인가해서 같은 크기의 전류가 흘렀다고 한다면,

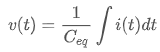
이라 할 수 있고, 위에서 정리된 키르히호프 전압 법칙 식과 결합하면,

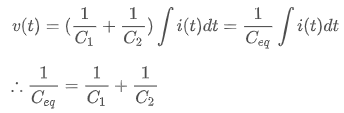
와 같이 정리할 수 있습니다. 다시 말해, 직렬로 연결된 커패시터를 하나의 커패시터로 합성할 경우 합성 커패시턴스 크기의 역수는 각 커패시턴스 크기의 역수를 합한 것과 같다는 것을 알 수 있지요.

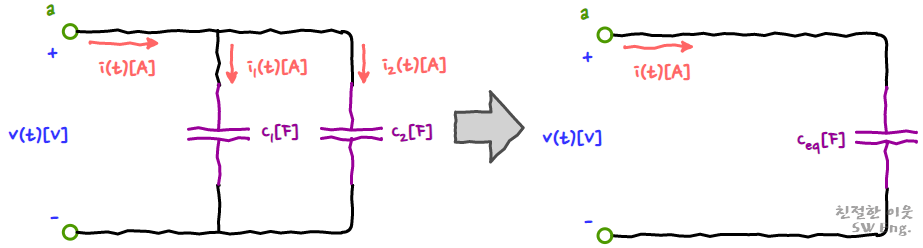
이번에는 병렬로 연결된 커패시터에 대한 합성 커패시턴스를 알아보겠습니다. 마찬가지로, 2개의 커패시터가 병렬로 연결된 회로에 전압 v(t)를 가해서 i(t)의 전류가 흘렀다고 한다면, 두 커패시터가 분기되는 지점에서 키르히호프의 전류 법칙에 따라 전류도 함께 분기될 것입니다. 각 커패시터의 마디로 분기된 전류를 i₁(t)와 i₂(t)라고 한다면,

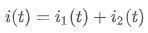
라는 키르히호프 전류 법칙에 관한 식을 얻을 수 있구요. 두 커패시터는 병렬로 연결되어 있으므로, 각각의 커패시터에는 회로 전체에 인가된 전압과 같은 크기의 전압이 걸리기 때문에,

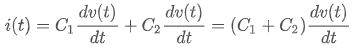
와 같이 정리할 수 있습니다. 그리고, 크기가 C_eq인 커패시터의 양단에 같은 크기의 전압을 인가해서 같은 크기의 전류가 흘렀다고 한다면, 커패시터의 전압, 전류 관계식을 키르히호프의 전류 법칙 식에 대입함으로써,

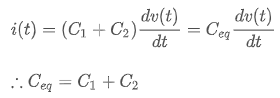
와 같이 정리할 수 있고, 이것으로 병렬로 연결된 커패시터를 하나의 커패시터로 합성할 경우 합성 커패시턴스의 크기는 각 커패시턴스의 합과 같다는 사실을 알 수 있습니다