지금까지 복잡한 회로를 해석하는 방법으로 중첩의 원리와 테브난 / 노턴의 등가 회로 변환을 알아보았습니다. 회로를 해석한다는 관점에서 이 방법들도 훌륭한 방법들인 것은 분명하지만, 해석을 위해 회로의 일부를 변경하는 등의 과정이 선행되어야 한다는 단점도 함께 가지고 있는데요. 회로를 있는 그대로 해석하는 2가지 방법이 있어서 같이 알아보도록 하겠습니다.

절점해석법
위 그림과 같은 회로에서 저항 R3로 흐르는 마디 전류의 크기는 저항 R3에 얼마의 전압이 걸리는지만 알면 옴의 법칙을 통해 간단히 계산할 수 있습니다.

다시 말해, 위 그림에서의 노드 b와 노드 d 사이의 전압을 알아내면 회로의 변환 없이도 원하는 마디 전류의 크기를 알 수 있다는 말인데요. 일단 이 회로에서는 전압원에 의한 전압 상승 또는 저항에 의한 전압 강하로 인해 전위차가 발생할 수 있는 노드를 4군데로 지정할 수 있습니다. 그리고 이 노드들에서의 전압을 각각 Va, Vb, Vc, Vd라고 지칭한다면, Vb을 제외한 나머지 노드에서의 전압이

라는 것을 알 수 있습니다.

노드 b를 중심으로, 노드 a로부터 유입되는 전류를 I1, 노드 c로부터 유입되는 전류를 I2라고 가정한다면, 키르히호프의 전류 법칙에 따라,

의 식을 얻을 수 있는데요. 여기서, 각 노드의 전압과 저항을 이용하여 옴의 법칙을 적용하면,

와 같은 식으로 변환할 수 있습니다. 여기에 미지수인 Vb를 제외한 나머지 값을 대입하면,

와 같이 Vb의 값을 구할 수 있지요. 그리고, 옴의 법칙을 적용하면,

와 같이 마디 전류의 크기를 계산할 수 있습니다. 정리하자면, 회로의 등가 변환 없이 전압 상승 또는 전압 강하가 일어나는 구간의 노드들을 중심으로 키르히호프의 전류 법칙을 이용해서 회로를 해석했는데요. 이런 방식으로 회로를 해석하는 방법이 절점해석법 또는 노드해석법입니다.
지금까지 설명드린 회로 해석 내용이 올바른지를 멀티심으로 확인해 보면,

와 같이, 절점해석법을 통한 결과와 같음을 확인할 수 있습니다.
망로해석법

같은 회로에 대해, 이번에는 다른 방법으로 해석을 해볼 건데요. 일단 회로를 가만히 들여다 보면, 저항 R3를 기준으로 왼쪽과 오른쪽에 루프가 형성되어 있는 것을 알 수 있습니다. 여기서 루프에 흐르는 전류의 크기를 I1과 I2이라고 가정한다면, 알고자 하는 전류 I는

이 되는데요. 여기서 루프 전류의 방향을 놓고 여러 반문이 나올 것 같습니다만, 일단 회로 해석을 끝까지 진행하고 나서 루프 전류에 대한 내용을 말씀드리도록 하겠습니다.
다시 내용으로 돌아와서, 루프 전류 I1과 I2에 따라 키르히호프 전압 법칙을 적용하면,

와 같은 루프 전류를 미지수로 하는 연립 방정식을 얻을 수 있습니다. 회로의 전압원과 저항의 크기를 위 방정식에 대입하면,

와 같이 루프 전류를 얻을 수 있구요. 계산한 루프 전류의 크기를

여기에 적용시키면,
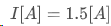
마디 전류의 크기를 계산할 수 있습니다.
이렇게 회로 내부의 루프마다 임의의 루프 전류를 정의하고, 여기에 대해 키르히호프의 전압 법칙을 이용해서 해석하는 방법을 망로해석법이라고 부릅니다.
이쯤에서 루프 전류라는 부분에 대해 다시 말씀을 드려야 하는데요. 루프 전류라는 것은 실제 회로에서 흐르는 전류를 의미하는 것이 아니고, 회로를 해석하기 위해 임의로 가정한 논리적인 전류를 의미합니다. 다시 말해, 루프 전류 I2의 경우에는 전압원의 극성과 반대로 되어 있으니까 잘못된 것이 아니냐고 반문하실 수도 있지만, 루프 전류를 정의하는 과정에서는 전압원의 극성이나 전류원의 방향 등은 전혀 중요한 요인이 아니기 때문에, 시계 방향으로 통일하는 경우가 대부분입니다. 대신에, 대신에 키르히호프의 전압 법칙을 적용할 때는 극성의 방향을 고려해서 적용해야 하지요. (위 연립 방정식의 ②번 식 참고...)
정리하자면, 어차피 키르히호프의 전압 법칙을 적용하는 과정에서 잘못 잡힌 루프 전류에 대한 방향이 보상되기 때문에 루프 전류의 방향을 놓고 왈가왈부할 필요가 없다는 말이구요. 실제로 전압원의 극성을 고려해서 I2의 방향을 거꾸로 두고 식을 다시 전개하더라도 같은 결과가 나오니까 엉뚱한 부분에서 힘 뺄 필요가 없다는 의미입니다. 하지만, 식을 전개해 나가는 과정에서 한 번 결정된 루프 전류의 방향은 끝까지 유지되어야 한다는 점 참고하시기 바랍니다.
