2단자 회로망

위 그림과 같은 회로에서 저항 R4에 얼마의 전압이 걸리는지를 알아보려면, 직병렬 관계로 복잡하게 연결된 저항들을 하나의 합성 저항으로 등가변환하는 작업을 선행한 다음, 옴의 법칙이나 전압 분배 법칙 등을 이용해서 계산해야 합니다. 그런데 여기서 저항 R4의 자리에 크기가 다른 저항을 연결한 상태에서 또 다시 걸리는 전압이나 전류 값을 알아내려면, 이전의 작업을 반복해서 수행해야 하지요.

그런데, 저항 R4가 단자 a와 단자 b를 갖는 2단자 회로망에 연결된 상태라고 가정하고, 단자 a, b의 왼쪽 부분을 하나의 전원과 하나의 저항을 가진 회로로 간략화 시킬 수 있다면, 저항에 걸리는 전압이나 공급 전류 등을 계산하기도 쉬워지고, 부하가 변경되어도 원하는 값을 찾아내기 수월해집니다.

이러한 2단자 회로망은 하나의 전압원과 내부 저항으로 구성된 전압 분배기, 또는 하나의 전류원과 내부 저항으로 구성된 전류 분배기로 간략화 시킬 수 있지요.
테브난의 정리
독일의 과학자 헬름홀트가 1853년에 처음으로 발견하고, 1883년 프랑스의 통신공학자 테브난에 의해 재발견된 테브난의 정리는 여러 전원과 저항들이 복잡하게 연결된 회로를 하나의 전압원과 하나의 직렬 저항으로만 구성된 간단한 전압 분배기의 형태로 등가 변환시키는 정리입니다.

처음 예로 들었던 회로에서, 저항 R4를 제외한 나머지 부분을 위 그림과 같이 테브난의 등가 회로로 변환해 보겠습니다. 앞에서 이야기한 대로, 테브난의 등가 회로는 하나의 전압원과 하나의 직렬 저항으로만 구성되므로, 변환 대상인 회로망으로부터 테브난 등가회로의 전압원과 직렬 저항의 크기를 구해주어야 합니다.
1) 전압원 구하기
단자 a와 b를 개방시킨 상태에서의 전위차가 테브난 등가회로에서의 전압원 크기가 됩니다.
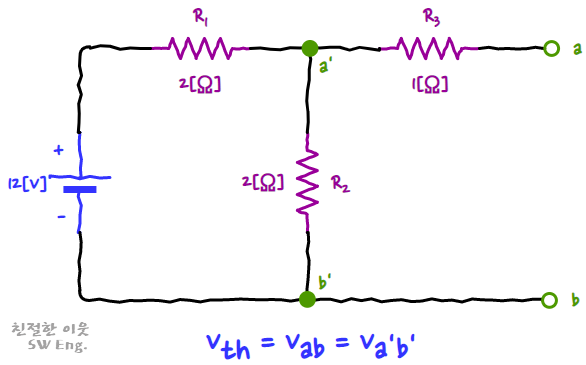
단자 a와 b가 개방된 상태에서 전위차인 Vab의 크기를 구하기 위해 회로를 들여다 보면, 저항 R2와 저항 R3가 병렬 연결 관계인 것을 알 수 있는데요. 그 말은, 단자 전압 Vab와 노드 a’와 b’ 사이의 전위차가 같다는 것을 알 수 있고, 개방 상태인 단자 a와 b로는 전기가 흐를 수 없으므로 직렬 연결된 저항 R1과 저항 R2의 회로에서 저항 R2에 걸리는 전압의 크기가 테브난 등가회로의 전압원 크기가 됩니다. 따라서, 저항 R1과 저항 R2는 모두 크기가 2[Ω]이므로, 전압 분배 법칙에 따라 저항 R2에는 6[V]의 전압이 걸리는 것을 알 수 있습니다.
2) 내부 저항 구하기
테브난 등가회로에서 내부 저항의 크기는 전원을 제거한 상태에서 단자 a, b로부터 들여다 보는 방향의 합성 저항 크기와 같습니다. 여기서 말하는 전원의 제거는 중첩의 원리에서 적용했던 전원 제거와 같은 방식으로 이루어지는데요. 전압원의 경우 단락, 전류원의 경우 개방시키는 것을 의미합니다.

따라서, 12[V] 크기의 전압원을 제거하면 위 그림과 같은 회로로 변환할 수 있구요. 단자 a, b 방향에서 바라본 합성 저항의 크기를 계산하면, 먼저 저항 R1과 저항 R2가 병렬로 연결된 상태이고, 이들의 합성 저항이 저항 R3와 직렬 연결되므로,

와 같이 계산할 수 있습니다. 즉, 테브난 등가 회로의 내부 저항은 2[Ω]이 된다는 말이지요.
지금까지의 내용을 멀티심을 이용해서 확인해 보면,
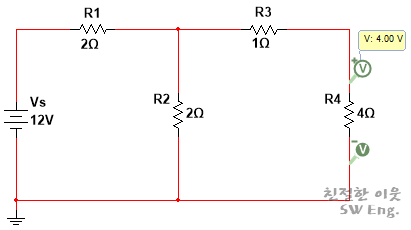
처음 예로 들었던 회로에서 저항 R4에 4[V]의 전압이 걸리는 것을 확인할 수 있구요.

앞에서 계산한 내용대로 테브난 등가 회로로 변환한 회로에서 걸리는 전압 역시 4[V]라는 것을 확인할 수 있습니다.
노턴의 정리
지멘스 할스케의 연구원 한스 페르디난트 마이어와 벨 연구소 공학자 에드워드 로리 노턴이 1926년에 서로 독자적으로 발표한 노턴의 정리는 여러 전원과 저항들이 복잡하게 연결된 회로를 하나의 전류원과 하나의 병렬 저항으로만 구성된 간단한 전류 분배기의 형태로 등가변환시키는 정리입니다.

같은 예제 회로에서, 저항 R4를 제외한 나머지 부분을 위 그림과 같이 노턴의 등가 회로로 변환해 보겠습니다. 앞에서 이야기한 대로, 노턴의 등가 회로는 하나의 전류원과 하나의 병렬 저항으로만 구성되므로, 변환 대상인 회로망으로부터 노턴 등가회로의 전류원과 병렬 저항의 크기를 구해 주어야 하는데요.
1) 전류원 구하기
단자 a와 b를 단락시킨 상태에서 흐르는 전류의 크기가 노턴 등가회로에서의 전류원 크기가 됩니다.

단자 a와 b 사이를 흐르는 전류의 크기를 구하기 위해,

먼저 저항 R2와 저항 R3의 합성 저항을 위와 같이 구할 수 있구요. 여기서 전압 분배 법칙을 이용하여, 합성 저항 R2||3에 걸리는 전압의 크기를

위와 같이 구한 다음, 옴의 법칙을 이용하여

단자 a와 b 사이를 흐르는 전류의 크기를 구할 수 있습니다.
2) 내부 저항 구하기
노턴의 등가회로에서도 내부 저항의 크기는 전원이 제거된 상태에서 단자 a, b로부터 들여다본 방향의 합성 저항 크기와 같습니다. 다시 말해, 테브난 정리에서 내부 저항을 구하는 방법과 노턴의 정리에서 내부 저항을 구하는 방법은 같다는 말이기 때문에, 이 부분에 대한 설명은 생략하겠습니다.
지금까지의 내용을 멀티심을 이용해서 확인해 보면, 예로 들었던 회로에서 저항 R4에 4[V]의 전압이 걸린다는 것은 테브난의 정리를 설명하는 과정에서 확인하였구요.

위에서 계산한 내용대로 노턴의 등가 회로를 적용했을 때, 저항 R4에 마찬가지로 4[V]의 전압이 걸린다는 것을 확인할 수 있다.
전원 변환
지금까지 살펴본 테브난의 정리나 노턴의 정리 모두, 2단자 회로망의 내부를 간단한 회로로 등가 변환 한다는 점에서 출발하였습니다. 그 말은 곧 테브난 등가 회로나 노턴의 등가 회로도 단자 a, b에 대해 서로 등가적인 관계라는 것을 의미하는데요. 이들이 실제로 등가적인 관계인지는 단자 a, b 사이에 임의의 저항 Rab를 연결했을 때 나타나는 전압과 전류 특성을 통해 확인할 수 있습니다. 그리고, 저항의 크기는 일반적으로 0과 ∞ 사이에 존재하므로, Rab = 0인 상황과 Rab = ∞ 인 상황이라는 극단적인 2가지 상황에서의 전압 및 전류 특성을 비교해보면 등가적인 관계 여부를 간단히 확인할 수 있겠지요.
1) Rab = 0인 상황: 단락 상태
저항 Rab의 크기가 0이라는 것은 단자 a, b가 단락되어 있음을 의미하는데요. 단락 상태에서는 전위차를 확인할 수 없으므로 흐르는 전류에 대한 부분만 확인해 볼 수 있습니다.

테브난의 등가 회로에서 단자 a, b를 단락시켰을 때 흐르는 단자 전류 Iab는 옴의 법칙만 적용해서 간단히 3[A]임을 알 수 있습니다. 반대로, 노턴의 등가 회로에서는 단자 a, b를 단락시킬 경우 단자 사이의 저항이 0[Ω]이 되므로, 전류 분배 법칙에 따라 전류원의 모든 전류가 단자 a, b로 흐르게 되면서, 테브난의 등가 회로에서와 같은 크기의 단자 전류가 흐른다는 것을 알 수 있습니다.
2) Rab = ∞인 상황: 개방 상태
저항 Rab의 크기가 ∞라는 것은 단자 a, b가 개방되어 있음을 의미하는데요. 개방 상태에서는 전류가 흐를 수 없으므로, 단자 사이의 전위차에 대한 부분만 확인해 볼 수 있습니다.

테브난의 등가 회로에서는 단자 a, b가 개방된 상태이기 때문에, 전압원의 (+) 극과 (-) 극 사이를 전하가 이동할 수 없습니다. 전하의 이동이 없다는 것은 어떠한 전압 강하도 일어나지 않는다는 것을 의미하므로, 전압원의 크기와 같은 크기의 전위차가 단자 a, b 사이에 나타납니다. 반대로, 노턴의 등가 회로에서는 단자 a, b의 전위차와 저항 Rno에 걸리는 전압의 크기가 같으므로, 옴의 법칙을 이용해서 계산하면 6[V]의 전압이 걸린다는 것을 알 수 있습니다.
지금까지의 과정을 통해 테브난의 등가 회로와 노턴의 등가 회로가 단자 a, b에 대해 서로 등가적인 관계라는 것을 알 수 있구요.

그리고, 위 식과 같은 관계가 형성되는 것 또한 자연스럽게 알 수 있습니다.
'Fundamentals > 회로이론' 카테고리의 다른 글
| 절점해석법과 망로해석법 (0) | 2021.02.28 |
|---|---|
| 전력 (0) | 2021.02.26 |
| 중첩의 원리 (0) | 2021.02.24 |
| 합성 저항과 키르히호프 법칙 (0) | 2021.02.23 |
| 전압, 전류, 저항... 그리고 옴의 법칙 (0) | 2021.02.21 |
