키르히호프 전압 법칙
회로 해석에 있어서 옴의 법칙 만큼이나 유명하면서 널리 활용되는 법칙 중 하나가 키르히호프 법칙입니다. 독일의 물리학자인 구스타프 키르히호프가 정립한 전기 회로에 관한 법칙으로, 전압에 관한 법칙과 전류에 관한 법칙으로 구분되지요.

위 그림과 같은 회로를 예로 들어서 생각해 봅시다. 이 회로에는 크기가 VS[V]인 전압원 하나와 크기가 R1[Ω], R2[Ω]인 저항이 하나씩 포함되어 있는데요. 전압원과 저항들을 위 그림과 같이 연결해서 하나의 폐회로를 구성할 수 있습니다. 그렇게 되면 전압원이 회로에 포함되어 있기 때문에, 크기가 I [A]인 전류가 흐르게 되겠지요.
전류가 흐른다는 것은 전압원의 (+) 극에서 출발한 전하가 (-) 극으로 회로를 따라 이동하는 것을 의미 (어디까지나 회로 해석에서의 전류 방향이 그렇다는 의미입니다.)합니다. 그리고 이 과정에서 또 다른 전압원을 만날 수도 있고 저항을 만날 수도 있는데요. 전압원을 만나게 되면 전압이 상승하게 되고, 저항을 만나게 되면 전압이 떨어지게 됩니다. 이것을 전압 상승 및 전압 강하라고 부르는데요. 이렇게 회로를 따라 이동하는 전하에서 발생하는 전압 상승 및 강하의 총 합은 언제나 0이 된다는 것이 키르히호프의 전압 법칙입니다. 다시 말해서, 크기가 VS[V] 만큼의 에너지를 갖고 출발한 전하들은 폐회로를 일주하는 과정에서 갖고 있던 에너지를 모두 소모하고, 전압원의 반대 극으로 돌아올 때는 0[V]로 돌아온다는 것이 키르히호프 전압 법칙의 기본적인 룰이라고 말씀드릴 수 있습니다.
이 내용을 기억하면서 위 그림의 회로를 전류의 방향에 따라 다시 한번 들여다 보면, 전압원의 (+) 극에서 VS[V] 만큼의 에너지를 가진 상태로 출발한 전하들이 저항 R1과 R2에서 에너지를 까먹고 돌아온다는 말인데요. 각각의 저항에서 까먹는 전압 강하량을 V1[V], V2[V]라고 정의하고, 이 회로에 I [A]의 전류가 흘렀다고 한다면,

와 같이, 옴의 법칙에 따라 각 저항에서 일어나는 전압 강하량을 계산할 수 있구요. 키르히호프의 전압 법칙에 따라

의 식을 얻을 수 있습니다. 여기서, 두 저항의 크기를 합한 부분을

으로 치환하면,

이렇게 식을 변환할 수 있습니다.

따라서, 마지막으로 변환된 식을 옴의 법칙으로 해석하면 위 그림과 같은 회로로 변환할 수 있구요. 여러 개의 저항이 연결된 회로를 하나의 합성 저항만 연결된 회로로 변환할 수 있는데, 직렬로 연결된 저항의 경우에는 합성 저항의 크기가 각 저항의 크기를 모두 합친 크기와 같다는 것을 알 수 있습니다.

다시 처음으로 돌아와서, 이번에는 각 저항에서의 전압 강하량에 초점을 맞춰서 회로를 해석해 봅시다.

합성 저항과의 관계를 통해 회로 전체에 흐르는 전류의 양을 위 식과 같이 정리할 수 있는데요. 여기서 전류의 양을 이용해서,
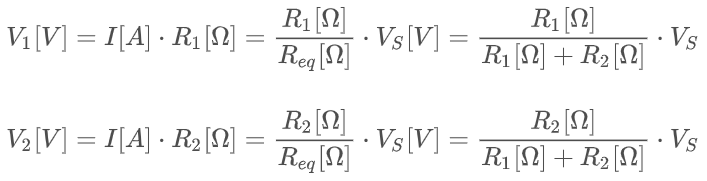
각 저항에서의 전압 강하량을 계산할 수 있습니다. 이렇게 정리된 내용을 통해, 저항이 직렬로 연결된 회로에서는 각 저항의 크기에 비례하여 전압 강하가 이루어진다는 것을 알 수 있구요. 이것을 전압 분배 법칙이라 부릅니다.
멀티심을 이용한 간단한 회로 시뮬레이션을 통해 지금까지의 내용을 다시 한 번 살펴보겠습니다.

위 그림과 같이 크기가 2[Ω]인 저항 R1 과 크기가 3[Ω]인 저항 R2가 직렬로 연결된 회로에 10[V]의 전압을 인가하였습니다. 프로브를 이용해서 각 저항에서 발생하는 전압 강하량을 측정해 보면, 키르히호프의 전압 법칙에 따라 각 저항에 대한 전압 강하량의 합과 공급 전압원의 크기가 같다는 것을 확인할 수 있구요. 각 저항에서의 전압 강하량은 저항의 크기와 비례한다는 것도 확인할 수 있습니다.
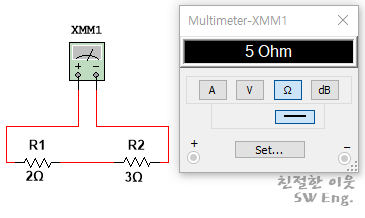
아울러, 직렬로 연결된 저항의 전체 크기를 멀티메터로 측정해보면, 두 저항의 합과 같은 크기라는 것도 확인할 수 있습니다.
키르히호프 전류 법칙
이번에는 키르히호프의 또 다른 법칙인 전류 법칙에 대해 알아보겠습니다.

위 그림과 같이 2개의 저항이 병렬로 연결된 회로를 예로 들어보겠습니다. 저항이 병렬로 연결되어 있으므로, 노드 a에서 저항 R1과 R2로 분기되는데요. 그리고 노드 b에서 다시 하나로 모이게 됩니다. 키르히호프의 전압 법칙에서는 전압원에서 출발한 전하들이 모두 하나의 길을 따라 이동했기 때문에 같은 양의 전하들이 각 저항들을 통과했지만, 위 그림의 회로에서는 노드 a에서 두 갈레로 갈라지기 때문에 각 저항으로 분기된 라인을 따라 전하들이 나눠져서 이동하게 됩니다. 다시 말해 병렬 연결에서는 전류가 분산되는 현상이 일어난다는 말이지요.
그렇다는 것은 노드 a의 관점에서 봤을 때, 전압원 방향으로부터 흘러들어 오는 I [A] 크기의 전류가 저항 R1과 R2가 연결된 마디로 나눠져서 흐르는데, 각 마디로 나눠진 전류의 총 합과 흘러들어온 전류의 크기는 당연히 같을 것이구요. 노드 b의 관점에서 본다면, 각 마디에서 흘러들어 오는 I1[A]과 I2[A] 크기의 전류가 노드 b를 통과하면서 하나로 합쳐지게 되는데, 이 때 전류의 크기 또한 당연히 같을 것입니다. 이렇게 하나의 노드를 기준으로, 연결된 모든 마디로 흘러들어오는 전류의 총 합과 흘러나가는 전류의 총 합이 같다는 것이 키르히호프의 전류 법칙입니다.
이번에는 위 그림의 회로를 키르히호프의 전압 법칙의 관점에서 다시 생각해 봅시다. 전압원에서 VS[V] 만큼의 에너지를 갖고 출발한 전하들이 회로를 따라 이동하던 중에 노드 a에서 두 방향으로 분기가 되면서 전하들도 양쪽으로 나눠져서 이동하게 됩니다. 하지만, 노드 b 이후에는 어떠한 저항도 연결되어 있지 않기 때문에 어느 마디로 전하가 이동하든 관계 없이, 키르히호프의 전압 법칙에 따라 전하가 가지고 있던 에너지를 모두 소모하고 통과하게 됩니다. 다시 말해서, 저항 R1과 R2에서의 전압 강하량은

전압원의 크기와 같다는 것을 알 수 있지요. 여기서 각 마디에 흐르는 전류를 각각 I1과 I2라고 한다면, 키르히호프의 전류 법칙에 따라,

의 관계식을 얻을 수 있는데요. 옴의 법칙을 이용하면,

과 같이 정리할 수 있고,
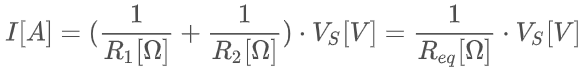
저항 부분을 위 식과 같이 Req으로 치환한다면,

와 같은 회로로 등가 변환할 수 있습니다. 따라서, 여러 개의 저항이 병렬로 연결된 경우에는 각 저항의 역수를 모두 합친 다음에 다시 역수화 시킨 것과 같다고 정리할 수 있습니다. 이번에는 위 식을

으로 변환한 후 각 마디 전류에 대한 옴의 법칙 관계식에 대입하면,

으로 정리할 수 있구요. 합성 저항 Req를

각각의 마디 전류 식에 대입하면

의 식을 얻을 수 있습니다. 따라서, 저항이 병렬로 연결된 회로에서는 각 마디로 분기되는 전류의 크기가 저항의 상대적인 크기에 반비례 한다는 것을 알 수 있구요. 이것을 전류 분배 법칙이라 부릅니다.
멀티심을 이용한 간단한 회로 시뮬레이션을 통해 지금까지의 내용을 다시 한번 살펴보겠습니다.

위 그림과 같이 크기가 2[Ω]인 저항 R1 과 크기가 6[Ω]인 저항 R2가 병렬로 연결된 회로에 12[V]의 전압을 인가하고, 프로브를 이용해서 회로 전체에 흐르는 전류와 각 저항이 연결된 마디에 흐르는 전류를 측정해보면, 키르히호프의 전류 법칙에 따라 전류가 분배되는 것을 확인할 수 있구요. 각 마디로 분배되는 전류의 크기는 저항의 상대적인 크기에 반비례하는 것도 확인할 수 있습니다.


아울러, 병렬로 연결된 저항의 전체 크기를 멀티메터로 측정해보면, 위 식과 같이 계산된 크기와 동일한 것을 확인할 수 있습니다.
'Fundamentals > 회로이론' 카테고리의 다른 글
| 절점해석법과 망로해석법 (0) | 2021.02.28 |
|---|---|
| 전력 (0) | 2021.02.26 |
| 테브난과 노턴의 정리 (0) | 2021.02.24 |
| 중첩의 원리 (0) | 2021.02.24 |
| 전압, 전류, 저항... 그리고 옴의 법칙 (0) | 2021.02.21 |
