R-L, R-C 회로의 DC 전원 응답

인덕턴스와 커패시턴스에 대한 특성을 설명하는 과정에서,

R - L 소자가 직렬로 연결된 직류 회로에서의 위 그림과 같은 응답 특성과

R - C 소자가 직렬로 연결된 직류 회로에서의 응답 특성을 설명드렸었는데요. 이러한 회로의 응답 특성을 이해하기 위해서는 먼저 시정수에 관한 내용을 짚고 넘어가야 합니다.

---

시정수

1차 선형 시스템에 스텝 함수 형태의 입력이 들어오게 되면,

와 같은 지수 함수 형태의 응답 특성을 보입니다. (여기서, Y_n은 정상 상태 값, Y₀은 초기 상태 값, 그리고 τ는 시정수...)

이러한 1차 선형 시스템의 응답 특성은 시간이 지남에 따라 정상상태에 접근은 하지만 도달하지는 못하는 특성을 보이는데요. 그래서 시스템의 응답 속도를 비교할 때 시정수를 사용합니다.

시스템의 응답 속도를 비교하는데 시정수를 사용하는 것은 시정수가 시스템의 증가율 (또는 감소율)과 관련이 있기 때문인데요. 위 그림과 같이 서로 다른 시스템의 응답 특성을 보여주는 지수 함수가 2개 있다고 가정해 봅시다. 이들의 초기 상태인 f(0)와 g(0)에서, 접선에 대한 직선 함수의 기울기는 시스템의 초기 변화율이라고 할 수 있는데요. 만약에, 이들 시스템이 초기 변화율을 그대로 유지한 상태로 계속 변화했다면, f(t)는 1초 후에, g(t)는 2초 후에 정상 상태에 도달하게 될 것입니다. 이 때 시정수는 시스템이 초기 변화율로 응답했을 때 정상 상태에 도달하는 시간을 의미하구요. 자연 대수 e의 지수 파트 절대값을 1로 만드는 값이며, 시스템의 정상 상태 기준으로 약 63.2%에 도달하는데 소요되는 시간을 의미합니다.

---

R-L 회로의 DC 전원 응답

위 그림과 같이 크기가 R인 저항과 크기가 L인 인덕터가 직렬로 연결된 회로에 크기가 V[V]인 직류 전압을 인가하였다고 가정하면, 인덕턴스에 대한 글에서도 설명드렸듯이, 인덕터의 양단에 공급 전압 만큼의 역기전력이 유도되면서 전류의 흐름을 차단하였다가, 서서히 역기전력이 감소하면서 정상상태 (인덕턴스의 성분이 무시되는 상태)에 도달하게 됩니다.

일단, 위 그림의 회로에 키르히호프의 전압 법칙을 적용하면,

과 같은 관계식을 얻을 수 있구요.

관계식의 양변을 적당히 정리해서 위와 같이 변형한 다음 적분해주면,

를 얻을 수 있습니다. 여기서, 초기 상태 (t = 0)에서 전류 값은 0이므로,

가 되구요. 이것을 다시 이전의 식에 대입한 다음,

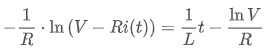
다음과 같이 식을 정리해 줄 수 있습니다.

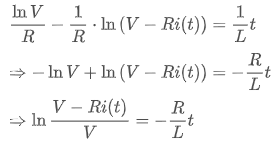
자연로그의 특성에 따라,

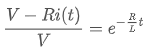
이므로,

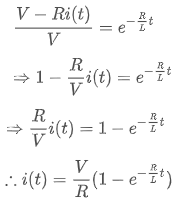
와 같이 양변을 적당히 정리하면, 전류의 관계식을 유도할 수 있습니다. 앞에서 이야기한대로, 자연대수 e의 지수 파트를 절대값 1로 만들어주는 것이 시정수이므로, R - L 회로에서 시정수 τ는

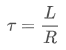
임을 알 수 있습니다.

지금까지의 내용을 지난 글에서 실행한 시뮬레이션 결과와 비교해보면,

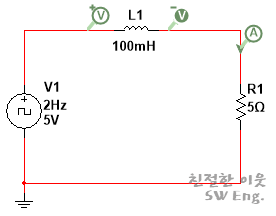
인덕턴스의 크기가 0.1[H]이고, 저항의 크기가 5[Ω]이므로, 이 회로의 시정수 τ는 0.02[sec]가 됩니다.

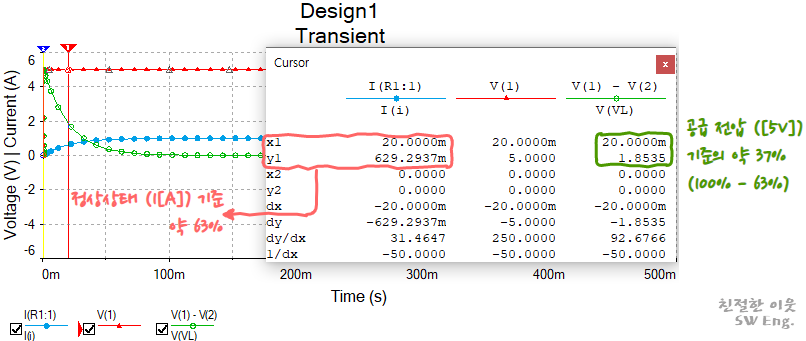
그리고, 시뮬레이션의 결과에서도 시정수인 20[ms]의 위치에서 정상상태 (1[A]) 대비 63% 수준의 전류가 흐른다는 것을 확인할 수 있습니다.

---

R-C 회로의 DC 전원 응답

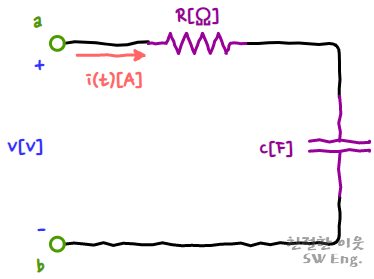
이번에는 위 그림과 같이 크기가 R인 저항과 크기가 C인 커패시터가 직렬로 연결된 회로에 크기가 V[V]인 직류 전압을 인가하였다고 가정하면, 커패시턴스에 대한 글에서 설명드렸듯이, 서서히 커패시터 양단에 전위차가 생겨나면서 정상상태 (커패시터가 마치 스위치를 차단한 것과 같은 상태)에 도달하게 됩니다.

위 회로에 키르히호프의 전압 법칙을 적용하면,

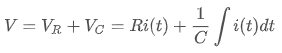
의 관계식을 얻을 수 있구요. 여기서, 양변을 미분해주면,

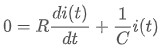
와 같이 식이 변형되고, 다음과 같이 양변을 적당히 정리해 줄 수 있습니다.

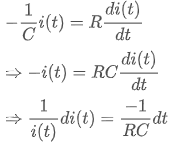
이렇게 정리된 식을

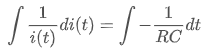
와 같이 적분해주고, 그 결과를

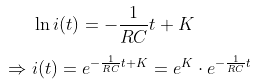
와 같이 정리할 수 있구요. 초기 상태 (t = 0)에서는 커패시터에 축적된 전하가 없으므로 회로에 흐르는 전류의 크기는

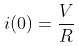
저항과 회로에 걸리는 전압에 대한 옴의 법칙 결과와 같습니다. 따라서,

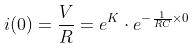
으로 정리할 수 있구요.

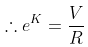
이 되니까, 결국 전류에 대한 관계식은

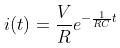
로 정리되고, 자연대수 e의 지수 파트의 절대값을 1로 만들어주는 시정수 τ는

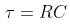
이 됩니다.

지금까지의 내용을 지난 글에서 실행한 시뮬레이션 결과와 비교해보면,

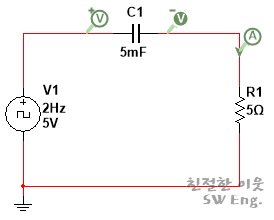
커패시턴스의 크기가 5[mF]이고, 저항의 크기가 5[Ω]이므로, 이 회로의 시정수 τ는 0.025[sec]가 됩니다.

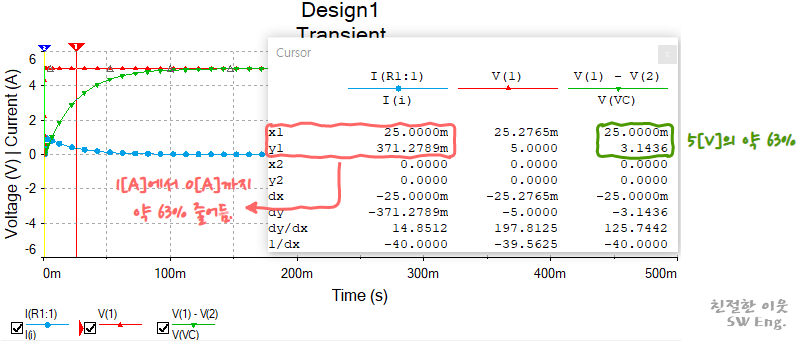
그리고, 시뮬레이션의 결과에서도 시정수인 25[ms]의 위치에서 전압, 전류 모두 정상상태 대비 63% 수준에 도달하는 것을 확인할 수 있습니다.