페이저
지금까지 교류 회로에 대한 해석을 진행할 때, 전압이나 전류를 사인 함수가 적용된 순시값으로 표현했었구요. 수동 소자들의 동작 특성 또한 사인 함수 그대로 해석을 했었습니다. 그러다보니, 미분과 적분을 해주는 상황이 번갈아 가면서 나타나다 보니, 미적분을 아직 정확히 이해하지 못한 사람들에게는 교류 회로 자체가 해석하기 상당히 어려운 난제처럼 느껴질 수 있습니다.
영국의 공학자인 올리버 헤비사이드는

의 식이 성립한다는 것에서 출발하여,

라는 수학적으로는 말도 안되는 내용이지만, 각 소자의 특성을 해석하는 식의 미분 파트에 대입해서,
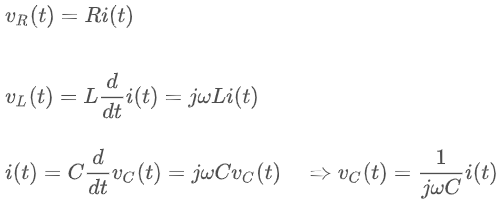
와 같이 정리한 다음에, 이들을 키르히호프의 전압 법칙에 적용해서

와 같은 복소수 형태의 임피던스를 유도하였습니다. 그리고 이런 복소 임피던스는

실수 축이 x축이고, 허수 축이 y축인 복소 평면에 표현할 수 있구요.

위 그림과 같이 삼각함수 형태로 표현할 수 있으며,
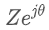
오일러의 공식에 따라, 위 그림의 식으로도 변환할 수 있습니다.

라는 수학적으로 말이 안되는 지점에서 출발한 내용이지만, 올리버 헤비사이드의 이런 이론은 교류 회로의 여러 많은 해석과 일치하는 결과를 보였구요. 특히나 미적분 없이 대수학적인 방식으로도 쉽게 해석할 수 있는 방법을 만들었다는 점에서 높은 의의를 가지고 있습니다. 이것은 임피던스가 아닌 교류 전압이나 교류 전류에도 같이 적용할 수 있는데요.

위 그림과 같이 저항과 인덕터, 그리고 커패시터가 직렬로 연결된 R-L-C 회로에 크기가 v(t)[V]인 교류 전압을 연결하여,

와 같은 교류 전류가 흘렀다면,

와 같이, θ만큼의 위상차를 갖는 교류 전압이 인가되었을 것입니다. 이들 교류 전류나 교류 전압의 경우에는 특별한 문제가 없는 이상, 진폭이나 위상, 그리고 주기가 변하지 않는 상태에서 위상차이만 가진 사인 함수의 특성을 그대로 보일 것인데요.

이들의 파형을 같은 시간축을 기준으로 겹쳐보면, 위 그림과 같이 표현될 것입니다. 즉, 일정한 위상 차이를 유지한 상태로 각각의 진폭만큼 증가와 감소를 반복하는 모습을 보일텐데요. 왼쪽의 그림처럼 각각의 진폭을 반지름으로 하는 원의 형태로도 표현될 수 있습니다.

이것을 앞에서 이야기한 올리버 헤비사이드의 방식으로,

와 같이 표현할 수 있구요. 그리고, 이것을 페이저라고 부릅니다. 즉, 진폭과 위상, 그리고 주기가 변하지 않는 사인 함수를 위상의 관점에서 표현한 것이 페이저이구요. 페이저를 통해 복잡한 삼각함수의 연산이나 미적분을 활용하지 않더라도 교류 회로를 쉽게 해석할 수 있습니다.

다음과 같이 크기가 20[Ω]인 저항과 1[mH]인 인덕터, 그리고 500[μF]인 커패시터를 직렬로 연결한 회로가 있구요. 여기에 병렬로 복소 임피던스를 정의하는 블록을 멀티심에서 연결하였습니다. 3개의 수동 소자에 대한 복소 임피던스를 각각 ZR, ZL, ZC라고 정의하고, 앞에서 설명드린 내용에 따라 각각의 복소 임피던스를 계산해 보면,

이 됩니다. 3개의 수동 소자를 모두 직렬로 연결하였으므로, 이들의 합성 복소 임피던스의 크기는

이 되구요. 이렇게 확인한 합성 복소 임피던스의 크기를 멀티심의 복소 임피던스 블록에 정의한 다음에 시뮬레이션을 실행시켜 보면

계산상 발생할 수 있는 범위의 오차 수준으로, 거의 비슷한 마디 전류가 흐름을 확인할 수 있습니다.
'Fundamentals > 회로이론' 카테고리의 다른 글
| 역률과 무효율 (0) | 2021.03.21 |
|---|---|
| 교류회로의 소비 전력 (0) | 2021.03.13 |
| 교류 회로의 합성 임피던스 (0) | 2021.03.06 |
| 교류 회로에서 수동 소자들의 특성 (0) | 2021.03.05 |
| 순시값, 최대값, 평균값, 실효값 (0) | 2021.03.03 |
